Simple Harmonic Motion (SHM)

Oct 24, 2024 — Mejbah Ahammad

Simple Harmonic Motion (SHM) Detailed Documentation

Simple Harmonic Motion (SHM)

Simple Harmonic Motion (SHM) is a fundamental concept in physics that describes the oscillatory motion of an object about an equilibrium position. It is characterized by its sinusoidal motion, where the restoring force is directly proportional to the displacement but acts in the opposite direction. Understanding SHM is crucial as it applies to a wide range of physical systems, from the vibrations of atoms in a crystal lattice to the oscillations of a pendulum in a clock.

Key Points of SHM

⏳🔄Periodic Motion
SHM represents periodic motion, meaning the motion repeats itself at regular intervals of time. The object moves back and forth over the same path, with each complete to-and-fro motion constituting one cycle or oscillation.

Mathematically, this periodicity is represented by sinusoidal functions like sine and cosine, which inherently repeat every $ 2\pi $ radians.
🏹⬅️Restoring Force
A key characteristic of SHM is the presence of a restoring force that is proportional to the displacement from equilibrium and acts in the opposite direction. This force tries to bring the object back to its equilibrium position.

This is expressed by Hooke's Law for springs:

$$ F = -k x $$

Where:
- $ F $ is the restoring force.
- $ k $ is the force constant (spring constant).
- $ x $ is the displacement from equilibrium.
📐🏃‍♂️💨Displacement, Velocity, and Acceleration
Displacement ($ x $): The distance and direction from the equilibrium position. It varies sinusoidally with time.

Velocity ($ v $): The rate of change of displacement with respect to time. It reaches its maximum at the equilibrium position and is zero at the extreme positions.

Acceleration ($ a $): The rate of change of velocity with respect to time. It is proportional to the negative of the displacement, always pointing toward the equilibrium position.
📏📊Amplitude (A)
The amplitude is the maximum displacement from the equilibrium position. It indicates the extent of oscillation and is a measure of the energy stored in the system. In ideal SHM, the amplitude remains constant over time.
⏰🔁Angular Frequency
The angular frequency ($ \omega $) represents how quickly the object oscillates. It is related to the period and frequency of the motion and is measured in radians per second.

The relationships are:

$$ \omega = 2\pi f = \dfrac{2\pi}{T} $$

Where:
- $ f $ is the frequency in hertz (Hz).
- $ T $ is the period in seconds.
🔄📈Phase Angle
The phase angle ($ \phi $) determines the initial state of the motion at time $ t = 0 $. It accounts for any initial displacement or velocity the object might have. The phase angle shifts the cosine or sine function horizontally on the time axis.
⚡️🔋Energy in SHM
In SHM, energy continually transforms between potential energy and kinetic energy, but the total mechanical energy remains constant (assuming no damping). At maximum displacement, the energy is entirely potential, and at the equilibrium position, it is entirely kinetic.
🌍🔍Real-Life Examples of SHM
- 🕰️Pendulum Clocks: The swinging pendulum regulates time through its periodic motion.
- 🛏️Mass-Spring Systems: Objects attached to springs oscillate when displaced from their equilibrium position.
- 🎸Musical Instruments: Guitar strings vibrate to produce sound waves, which are examples of SHM.
- 🎢Playground Swings: The to-and-fro motion of swings approximates SHM under small angles.

Mathematical Explanation of SHM

The mathematical description of SHM involves differential equations and trigonometric functions. The motion can be derived from Newton's laws and the characteristics of the restoring force.

Displacement as a Function of Time

The general equation for displacement in SHM is:

$$ x(t) = A \cos(\omega t + \phi) $$

Alternatively, a sine function may be used:

$$ x(t) = A \sin(\omega t + \phi) $$

The choice between sine and cosine depends on the initial conditions.

Understanding the Components

Amplitude ($ A $): Determines the maximum displacement.
Angular Frequency ($ \omega $): Determines how rapidly the oscillations occur.
Phase Angle ($ \phi $): Sets the initial position and direction of motion.

Velocity as a Function of Time

Velocity is the first derivative of displacement with respect to time:

\[ \begin{align*} v(t) &= \dfrac{dx}{dt} \\ &= -A \omega \sin(\omega t + \phi) \end{align*} \]

This shows that velocity is also a sinusoidal function, shifted by a phase of $ \dfrac{\pi}{2} $ radians relative to displacement.

Acceleration as a Function of Time

Acceleration is the derivative of velocity with respect to time, or the second derivative of displacement:

\[ \begin{align*} a(t) &= \dfrac{dv}{dt} \\ &= -A \omega^2 \cos(\omega t + \phi) \\ &= -\omega^2 x(t) \end{align*} \]

The negative sign indicates that acceleration is always directed opposite to displacement, confirming the presence of a restoring force.

Differential Equation of SHM

The equation of motion for SHM can be derived from Newton's second law and Hooke's Law:

\[ \begin{align*} F &= m a \\ F &= -k x \\ \therefore m a &= -k x \\ \implies a &= -\dfrac{k}{m} x \\ \implies \dfrac{d^2 x}{dt^2} + \dfrac{k}{m} x &= 0 \end{align*} \]

This is a second-order linear differential equation whose general solution is the sinusoidal function representing SHM.

Angular Frequency in SHM Systems

The angular frequency ($ \omega $) depends on the physical parameters of the system.

Mass-Spring System

For a mass-spring system:

$$ \omega = \sqrt{\dfrac{k}{m}} $$

Where:

$ k $ is the spring constant (N/m).
$ m $ is the mass attached to the spring (kg).

Simple Pendulum

For a simple pendulum (assuming small oscillations):

$$ \omega = \sqrt{\dfrac{g}{L}} $$

Where:

$ g $ is the acceleration due to gravity (approximately $ 9.81 \, \text{m/s}^2 $).
$ L $ is the length of the pendulum (m).

Period and Frequency

The period ($ T $) is the time taken for one complete oscillation. It is related to angular frequency by:

$$ T = \dfrac{2\pi}{\omega} $$

The frequency ($ f $) is the number of oscillations per unit time:

$$ f = \dfrac{1}{T} = \dfrac{\omega}{2\pi} $$

Energy Analysis in SHM

Understanding energy transformations in SHM provides insight into the dynamics of oscillatory systems.

Potential Energy ($ U $)

The potential energy in a mass-spring system is stored due to the displacement from the equilibrium position:

$$ U = \dfrac{1}{2} k x^2 $$

It reaches a maximum at maximum displacement and is zero at the equilibrium position.

Kinetic Energy ($ K $)

The kinetic energy is due to the motion of the mass:

$$ K = \dfrac{1}{2} m v^2 $$

It is maximum at the equilibrium position where velocity is greatest and zero at maximum displacement where the velocity is zero.

Total Mechanical Energy ($ E $)

The total mechanical energy remains constant in ideal SHM (no damping):

\[ \begin{align*} E &= U + K \\ &= \dfrac{1}{2} k x^2 + \dfrac{1}{2} m v^2 \\ &= \dfrac{1}{2} k A^2 \end{align*} \]

Since $ x = A \cos(\omega t + \phi) $ and $ v = -A \omega \sin(\omega t + \phi) $, substituting these into $ U $ and $ K $ shows that $ E $ is constant.

Proof of Energy Conservation

\[ \begin{align*} U &= \dfrac{1}{2} k x^2 = \dfrac{1}{2} k A^2 \cos^2(\omega t + \phi) \\ K &= \dfrac{1}{2} m v^2 = \dfrac{1}{2} m A^2 \omega^2 \sin^2(\omega t + \phi) \\ E &= U + K \\ &= \dfrac{1}{2} k A^2 \cos^2(\omega t + \phi) + \dfrac{1}{2} m A^2 \omega^2 \sin^2(\omega t + \phi) \\ &= \dfrac{1}{2} A^2 \left[ k \cos^2(\omega t + \phi) + m \omega^2 \sin^2(\omega t + \phi) \right] \end{align*} \]

Since $ \omega = \sqrt{\dfrac{k}{m}} $, it follows that $ m \omega^2 = k $. Therefore:

\[ \begin{align*} E &= \dfrac{1}{2} A^2 k \left[ \cos^2(\omega t + \phi) + \sin^2(\omega t + \phi) \right] \\ &= \dfrac{1}{2} A^2 k (1) \\ &= \dfrac{1}{2} k A^2 \end{align*} \]

Thus, the total mechanical energy is constant and depends only on the amplitude and the spring constant.

Detailed Examples of SHM

Example 1: Mass-Spring System

Consider a mass $ m = 2 \, \text{kg} $ attached to a spring with a spring constant $ k = 50 \, \text{N/m} $. The mass is displaced by $ A = 0.1 \, \text{m} $ from the equilibrium position and released.

Calculate the Angular Frequency ($ \omega $)

$$ \omega = \sqrt{\dfrac{k}{m}} = \sqrt{\dfrac{50}{2}} = \sqrt{25} = 5 \, \text{rad/s} $$

Determine the Period ($ T $) and Frequency ($ f $)

\[ \begin{align*} T &= \dfrac{2\pi}{\omega} = \dfrac{2\pi}{5} \approx 1.257 \, \text{s} \\ f &= \dfrac{1}{T} \approx \dfrac{1}{1.257} \approx 0.796 \, \text{Hz} \end{align*} \]

Equation of Motion

Assuming the mass is released from maximum displacement with zero initial velocity, the displacement equation is:

$$ x(t) = A \cos(\omega t) = 0.1 \cos(5t) $$

Velocity and Acceleration Equations

Velocity:

$$ v(t) = -A \omega \sin(\omega t) = -0.1 \times 5 \sin(5t) = -0.5 \sin(5t) $$

Acceleration:

$$ a(t) = -A \omega^2 \cos(\omega t) = -0.1 \times 25 \cos(5t) = -2.5 \cos(5t) $$

Energy Calculations

Total Mechanical Energy:

$$ E = \dfrac{1}{2} k A^2 = \dfrac{1}{2} \times 50 \times (0.1)^2 = 0.25 \, \text{J} $$

Potential Energy at $ t = 0 $:

$$ U = \dfrac{1}{2} k x^2 = 0.25 \, \text{J} $$

Kinetic Energy at $ t = 0 $:

$$ K = 0 \, \text{J} $$

Example 2: Simple Pendulum

A simple pendulum with length $ L = 0.5 \, \text{m} $ is displaced by a small angle and released.

Calculate the Angular Frequency ($ \omega $)

$$ \omega = \sqrt{\dfrac{g}{L}} = \sqrt{\dfrac{9.81}{0.5}} \approx \sqrt{19.62} \approx 4.43 \, \text{rad/s} $$

Determine the Period ($ T $)

$$ T = \dfrac{2\pi}{\omega} = \dfrac{2\pi}{4.43} \approx 1.42 \, \text{s} $$

Equation of Motion

If the pendulum is released from rest at a maximum angular displacement $ \theta_{\text{max}} = 0.1 \, \text{rad} $:

$$ \theta(t) = \theta_{\text{max}} \cos(\omega t) = 0.1 \cos(4.43 t) $$

Damped and Driven Harmonic Motion (Advanced Topic)

Real-world oscillating systems often experience damping (energy loss) and external driving forces. Understanding these factors extends the basic SHM model.

Damped Harmonic Motion

Damping causes the amplitude of oscillations to decrease over time due to energy loss (e.g., friction, air resistance). The equation of motion includes a damping term proportional to velocity:

$$ m \dfrac{d^2 x}{dt^2} + b \dfrac{dx}{dt} + k x = 0 $$

Where $ b $ is the damping coefficient.

Driven Harmonic Motion

An external periodic force can drive the system, leading to the equation:

$$ m \dfrac{d^2 x}{dt^2} + b \dfrac{dx}{dt} + k x = F_0 \cos(\omega_{\text{d}} t) $$

Where $ F_0 $ is the amplitude of the driving force and $ \omega_{\text{d}} $ is its angular frequency.

Resonance

When the driving frequency matches the natural frequency of the system ($ \omega_{\text{d}} \approx \omega_0 $), resonance occurs, leading to large amplitude oscillations.

Applications of SHM

SHM concepts are applied across various fields:

Acoustics

Sound waves are longitudinal waves resulting from SHM of air particles. Musical instruments use SHM to produce harmonious sounds.

Electronics

Electrical circuits containing inductors and capacitors exhibit SHM in the form of oscillating currents and voltages.

Quantum Mechanics

At the atomic level, particles exhibit SHM-like behavior in potential wells, leading to quantized energy levels.

Seismology

Earthquakes generate seismic waves that can be analyzed using SHM principles to understand the Earth's interior.

Conclusion

Simple Harmonic Motion is a cornerstone of classical mechanics, providing a framework for understanding oscillatory phenomena in nature. Its mathematical elegance and wide applicability make it an essential topic in physics and engineering. By mastering SHM, one gains valuable insights into the behavior of various systems and the underlying principles governing motion and energy.

From the gentle swing of a pendulum to the vibrations of molecules, SHM plays a vital role in explaining the rhythmic patterns observed in the physical world.

Understanding SHM not only enriches our knowledge of physics but also empowers us to harness oscillatory systems in technology, medicine, and industry.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

# Parameters for Simple Harmonic Motion (SHM)
A = 1.0         # Amplitude
omega = 2.0     # Angular frequency
phi = 0         # Phase angle
t_max = 10      # Max time
frames = 100    # Number of frames

# Time array
t = np.linspace(0, t_max, frames)

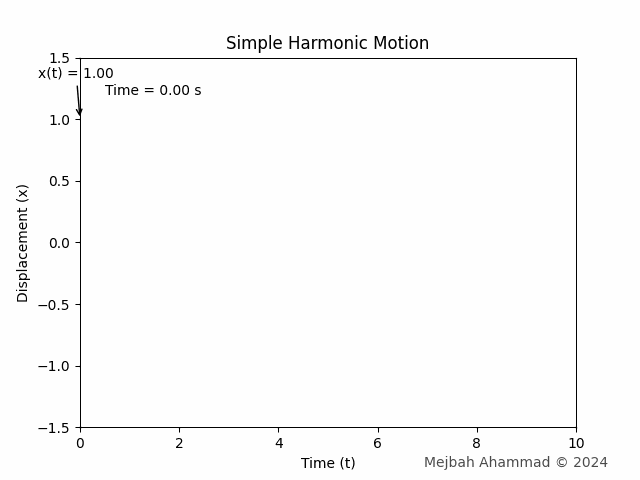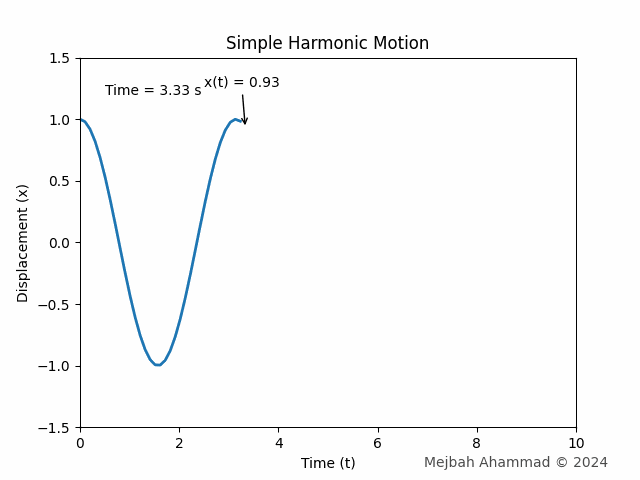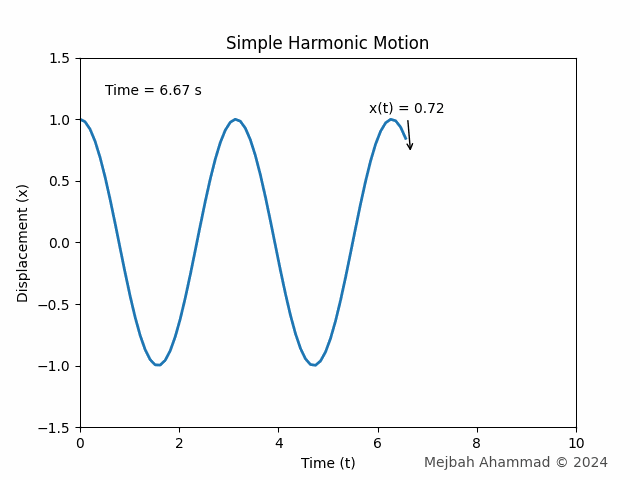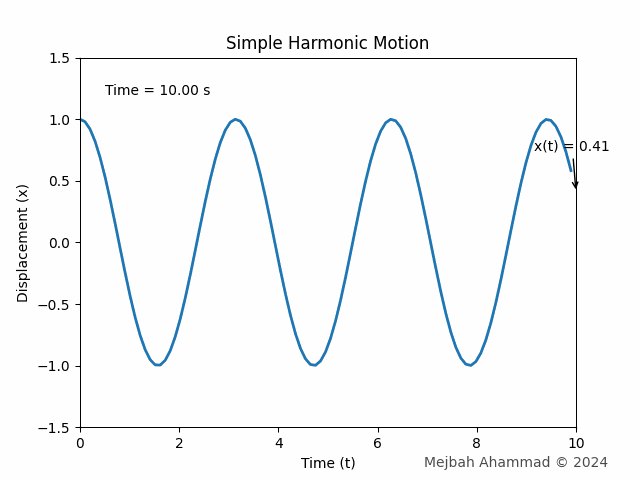
# SHM Equation: x(t) = A * cos(omega * t + phi)
x = A * np.cos(omega * t + phi)

# Create a figure and axis
fig, ax = plt.subplots()
ax.set_xlim(0, t_max)
ax.set_ylim(-1.5 * A, 1.5 * A)
ax.set_xlabel('Time (t)')
ax.set_ylabel('Displacement (x)')
ax.set_title('Simple Harmonic Motion')

# Line to update during the animation
line, = ax.plot([], [], lw=2, label='SHM')

# Initialize annotation and text
annotation = ax.annotate('', xy=(0, 0), xytext=(-30, 30), textcoords='offset points',
                         arrowprops=dict(arrowstyle='->'))
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes)

# Initialization function
def init():
    line.set_data([], [])
    annotation.set_text('')
    time_text.set_text('')
    return line, annotation, time_text

# Animation function
def animate(i):
    # Update the line plot
    line.set_data(t[:i], x[:i])
    
    # Update the annotation to move along with the particle
    annotation.xy = (t[i], x[i])
    annotation.set_text(f"x(t) = {x[i]:.2f}")
    
    # Update the time text
    time_text.set_text(f"Time = {t[i]:.2f} s")
    
    return line, annotation, time_text

# Create animation
anim = FuncAnimation(fig, animate, init_func=init, frames=frames, interval=100, blit=True)

# Save the animation as a GIF
anim.save('shm_dynamic_plot_animated.gif', writer='pillow')

# Display the final frame of the plot
plt.plot(t, x, label='SHM')
plt.legend()
plt.show()

Simple Harmonic Motion (SHM)

Key Points of SHM

Mathematical Explanation of SHM

Displacement as a Function of Time

Understanding the Components

Velocity as a Function of Time

Acceleration as a Function of Time

Differential Equation of SHM

Angular Frequency in SHM Systems

Mass-Spring System

Simple Pendulum

Period and Frequency

Energy Analysis in SHM

Potential Energy (\( U \))

Kinetic Energy (\( K \))

Total Mechanical Energy (\( E \))

Proof of Energy Conservation

Detailed Examples of SHM

Example 1: Mass-Spring System

Calculate the Angular Frequency (\( \omega \))

Determine the Period (\( T \)) and Frequency (\( f \))

Equation of Motion

Velocity and Acceleration Equations

Energy Calculations

Example 2: Simple Pendulum

Calculate the Angular Frequency (\( \omega \))

Determine the Period (\( T \))

Equation of Motion

Damped and Driven Harmonic Motion (Advanced Topic)

Damped Harmonic Motion

Driven Harmonic Motion

Resonance

Applications of SHM

Acoustics

Electronics

Quantum Mechanics

Seismology

Conclusion