Skip to main content

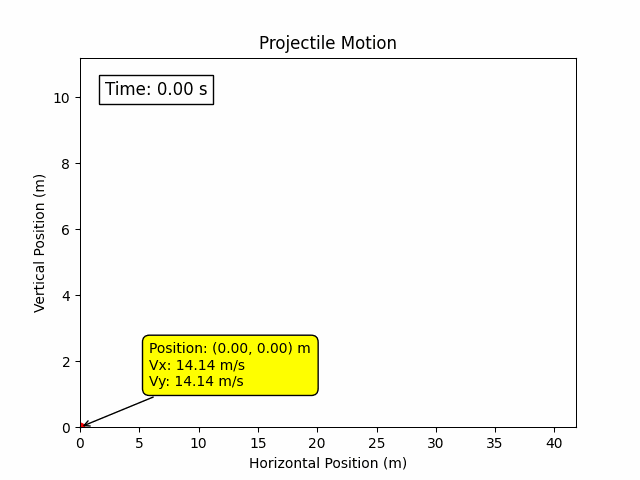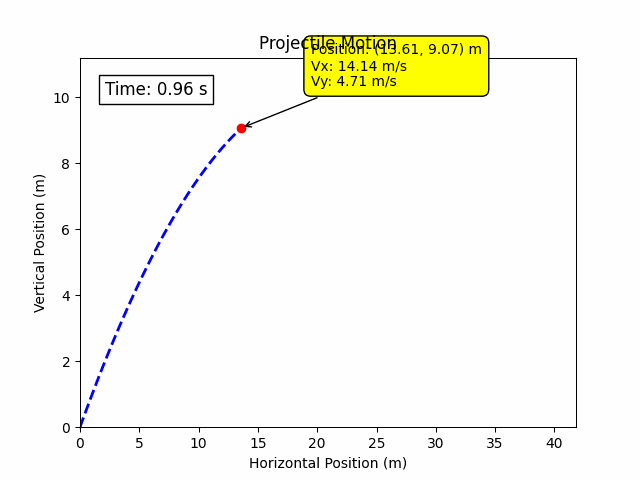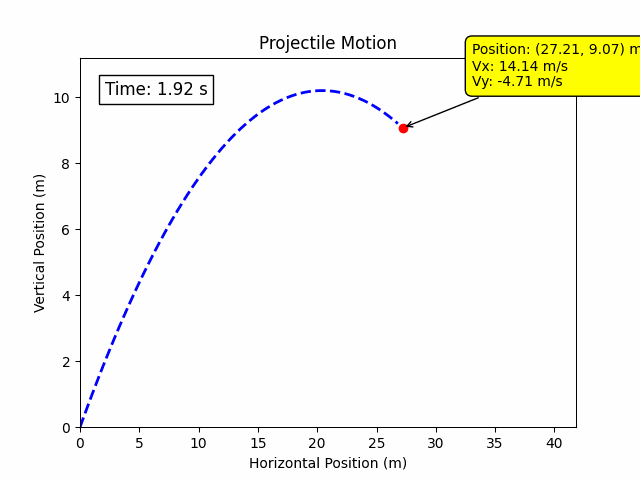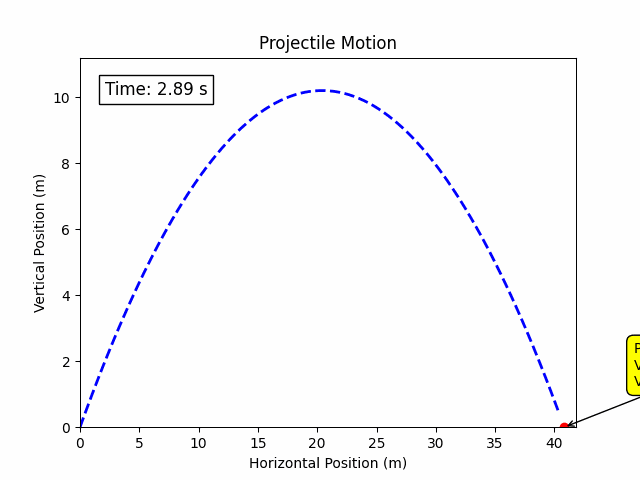
Pojectile Motion With Python

— Mejbah Ahammad

Pojectile Motion With Python

Projectile motion is a form of motion where an object moves in a bilaterally symmetrical, parabolic path under the action of gravity alone (assuming negligible air resistance). It is a fundamental concept in physics and engineering, essential for understanding the behavior of objects launched into the air, such as balls, bullets, or rockets.

Projectile Motion Icon

Key Concepts in Projectile Motion

  1. 🏹Definition of Projectile Motion

    A projectile is any object thrown into space upon which the only acting force is gravity. The motion involves two components:

    • Horizontal Motion: Constant velocity due to the absence of horizontal forces (neglecting air resistance).
    • Vertical Motion: Accelerated motion due to gravity acting downward.
  2. 🛠️Assumptions in Projectile Motion Analysis

    For simplification, the following assumptions are made:

    • Gravity is constant and acts downward at \( g = 9.8 \, \text{m/s}^2 \).
    • Air resistance is negligible.
    • The Earth's curvature and rotation are ignored.
  3. 📈Trajectory of a Projectile

    The path followed by a projectile is a parabola. The mathematical equation of the trajectory is:

    $$ y = x \tan \theta - \dfrac{g x^2}{2 v_0^2 \cos^2 \theta} $$

    Where:

    • \( y \) is the vertical position.
    • \( x \) is the horizontal position.
    • \( \theta \) is the initial launch angle.
    • \( v_0 \) is the initial launch speed.
  4. ⏱️Time of Flight

    The total time a projectile is in the air is given by:

    $$ T = \dfrac{2 v_0 \sin \theta}{g} $$
  5. 📏Maximum Height

    The highest vertical position reached by the projectile:

    $$ H = \dfrac{v_0^2 \sin^2 \theta}{2g} $$
  6. 🌐Horizontal Range

    The total horizontal distance traveled by the projectile:

    $$ R = \dfrac{v_0^2 \sin 2\theta}{g} $$
  7. ⚙️Equations of Motion

    The motion can be analyzed using kinematic equations:

    • Horizontal Motion: \( x = v_{0x} t \)
    • Vertical Motion: \( y = v_{0y} t - \dfrac{1}{2} g t^2 \)

    Where:

    • \( v_{0x} = v_0 \cos \theta \)
    • \( v_{0y} = v_0 \sin \theta \)

Mathematical Analysis of Projectile Motion

Projectile motion can be broken down into horizontal and vertical components, analyzed independently.

Horizontal Motion

The horizontal component is characterized by constant velocity:

$$ v_x = v_0 \cos \theta $$

Since there is no acceleration horizontally (assuming no air resistance):

$$ x = v_x t $$

Vertical Motion

The vertical component is subject to gravitational acceleration:

$$ v_y = v_0 \sin \theta - g t $$
$$ y = v_0 \sin \theta \, t - \dfrac{1}{2} g t^2 $$

Time of Flight Derivation

The time when the projectile returns to the original vertical position (\( y = 0 \)):

\[ \begin{align*} y &= v_0 \sin \theta \, t - \dfrac{1}{2} g t^2 = 0 \\ t (v_0 \sin \theta - \dfrac{1}{2} g t) &= 0 \\ t &= 0 \quad \text{or} \quad t = \dfrac{2 v_0 \sin \theta}{g} \end{align*} \]

The non-zero solution gives the total time of flight.

Maximum Height Derivation

The maximum height is reached when the vertical velocity is zero (\( v_y = 0 \)):

\[ \begin{align*} v_y &= v_0 \sin \theta - g t = 0 \\ t &= \dfrac{v_0 \sin \theta}{g} \end{align*} \]

Substitute \( t \) back into the vertical position equation:

\[ \begin{align*} H &= v_0 \sin \theta \left( \dfrac{v_0 \sin \theta}{g} \right) - \dfrac{1}{2} g \left( \dfrac{v_0 \sin \theta}{g} \right)^2 \\ &= \dfrac{v_0^2 \sin^2 \theta}{2g} \end{align*} \]

Horizontal Range Derivation

The horizontal range is calculated by multiplying horizontal velocity and total time of flight:

\[ \begin{align*} R &= v_x T \\ &= v_0 \cos \theta \left( \dfrac{2 v_0 \sin \theta}{g} \right) \\ &= \dfrac{2 v_0^2 \sin \theta \cos \theta}{g} \\ &= \dfrac{v_0^2 \sin 2\theta}{g} \end{align*} \]

Using the identity \( \sin 2\theta = 2 \sin \theta \cos \theta \).

Factors Affecting Projectile Motion

Initial Velocity (\( v_0 \))

Higher initial velocity increases the time of flight, maximum height, and horizontal range.

Launch Angle (\( \theta \))

The launch angle critically affects the trajectory:

  • At \( \theta = 45^\circ \), the projectile achieves maximum range.
  • Angles greater than \( 45^\circ \) result in higher maximum heights but shorter ranges.
  • Angles less than \( 45^\circ \) result in longer ranges but lower maximum heights.

Gravity (\( g \))

On planets with different gravitational acceleration, the projectile's behavior changes accordingly.

Examples of Projectile Motion

Example 1: Calculating Time of Flight and Range

A ball is thrown with an initial speed of \( 20 \, \text{m/s} \) at an angle of \( 30^\circ \) above the horizontal. Calculate the time of flight and the horizontal range.

Solution

Time of Flight:

\[ T = \dfrac{2 v_0 \sin \theta}{g} = \dfrac{2 \times 20 \times \sin 30^\circ}{9.8} = \dfrac{40 \times 0.5}{9.8} \approx 2.04 \, \text{s} \]

Horizontal Range:

\[ R = v_0 \cos \theta \times T = 20 \times \cos 30^\circ \times 2.04 = 20 \times 0.866 \times 2.04 \approx 35.36 \, \text{m} \]

Example 2: Maximum Height Calculation

An arrow is shot vertically upward with an initial speed of \( 50 \, \text{m/s} \). What is the maximum height reached?

Solution

Since the motion is vertical, \( \theta = 90^\circ \) and \( \sin 90^\circ = 1 \):

\[ H = \dfrac{v_0^2 \sin^2 \theta}{2g} = \dfrac{50^2 \times 1}{2 \times 9.8} = \dfrac{2500}{19.6} \approx 127.55 \, \text{m} \]

Projectile Motion with Air Resistance (Advanced Topic)

When air resistance is considered, the motion becomes more complex and is no longer symmetric.

Drag Force

Air resistance can be modeled as a drag force proportional to the velocity:

$$ \mathbf{F}_{\text{drag}} = -k \mathbf{v} $$

Where \( k \) is the drag coefficient and \( \mathbf{v} \) is the velocity vector.

Equations of Motion with Air Resistance

The differential equations become:

$$ m \dfrac{d v_x}{dt} = -k v_x $$
$$ m \dfrac{d v_y}{dt} = -m g - k v_y $$

Solution to Equations

The solutions involve exponential decay functions:

$$ v_x(t) = v_{0x} e^{- (k/m) t} $$
$$ v_y(t) = \left( v_{0y} + \dfrac{m g}{k} \right) e^{- (k/m) t} - \dfrac{m g}{k} $$

These equations require numerical methods or advanced calculus to solve for position and velocity at any time \( t \).

Applications of Projectile Motion

Sports

Understanding projectile motion helps athletes and coaches improve performance in sports like basketball, football, and archery.

Engineering and Ballistics

Engineers design trajectories for missiles, rockets, and other projectiles considering both gravity and air resistance.

Astronomy

Projectile motion principles apply to celestial bodies and spacecraft trajectories within gravitational fields.

Conclusion

Projectile motion is a key concept that illustrates the principles of two-dimensional motion under constant acceleration. By decomposing the motion into horizontal and vertical components, we can predict and analyze the trajectory of objects thrown or launched into the air.

Mastery of projectile motion concepts is essential for students and professionals in physics, engineering, sports science, and various technological fields.

Advancements in computational tools allow for more accurate modeling, including factors like air resistance, enhancing our ability to design and predict real-world projectile behavior.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

# Parameters for Projectile Motion
g = 9.8          # Acceleration due to gravity (m/s^2)
v0 = 20          # Initial velocity (m/s)
angle = 45       # Launch angle (degrees)
t_max = 2 * v0 * np.sin(np.radians(angle)) / g  # Total flight time
frames = 100     # Number of frames

# Time and space arrays
t = np.linspace(0, t_max, frames)
x = v0 * np.cos(np.radians(angle)) * t
y = v0 * np.sin(np.radians(angle)) * t - 0.5 * g * t**2

# Create the figure and axis
fig, ax = plt.subplots()
ax.set_xlim(0, max(x) + 1)
ax.set_ylim(0, max(y) + 1)
ax.set_xlabel('Horizontal Position (m)')
ax.set_ylabel('Vertical Position (m)')
ax.set_title('Projectile Motion')

# Line to update during the animation
line, = ax.plot([], [], lw=2, label='Trajectory', color='blue', linestyle='--')
point, = ax.plot([], [], 'o', color='red')  # Point for the projectile

# Enhanced annotation and time text
annotation = ax.annotate('', xy=(0, 0), xytext=(50, 30), textcoords='offset points',
                         bbox=dict(boxstyle='round,pad=0.5', fc='yellow', ec='black', lw=1),
                         arrowprops=dict(arrowstyle='->', color='black'))
time_text = ax.text(0.05, 0.9, '', transform=ax.transAxes, fontsize=12,
                    bbox=dict(facecolor='white', edgecolor='black'))

# Initialization function for the animation
def init():
    line.set_data([], [])
    point.set_data([], [])
    annotation.set_text('')
    time_text.set_text('')
    return line, point, annotation, time_text

# Animation function to update frame by frame
def animate(i):
    # Update the trajectory line
    line.set_data(x[:i], y[:i])

    # Update the projectile point
    point.set_data(x[i], y[i])

    # Update annotation to display current position and velocity components
    vx = v0 * np.cos(np.radians(angle))
    vy = v0 * np.sin(np.radians(angle)) - g * t[i]

    annotation.xy = (x[i], y[i])
    annotation.set_text(f"Position: ({x[i]:.2f}, {y[i]:.2f}) m\n"
                        f"Vx: {vx:.2f} m/s\n"
                        f"Vy: {vy:.2f} m/s")

    # Update the time text
    time_text.set_text(f"Time: {t[i]:.2f} s")

    return line, point, annotation, time_text
# Create the animation
anim = FuncAnimation(fig, animate, init_func=init, frames=frames, interval=100, blit=True)

# Save the animation as a GIF
anim.save('projectile_motion_enhanced_annotated.gif', writer='pillow')

# Display the final frame of the plot
plt.plot(x, y, label='Trajectory', color='blue', linestyle='--')
plt.scatter(x[-1], y[-1], color='red', label='Landing Point')
plt.legend()
plt.show()