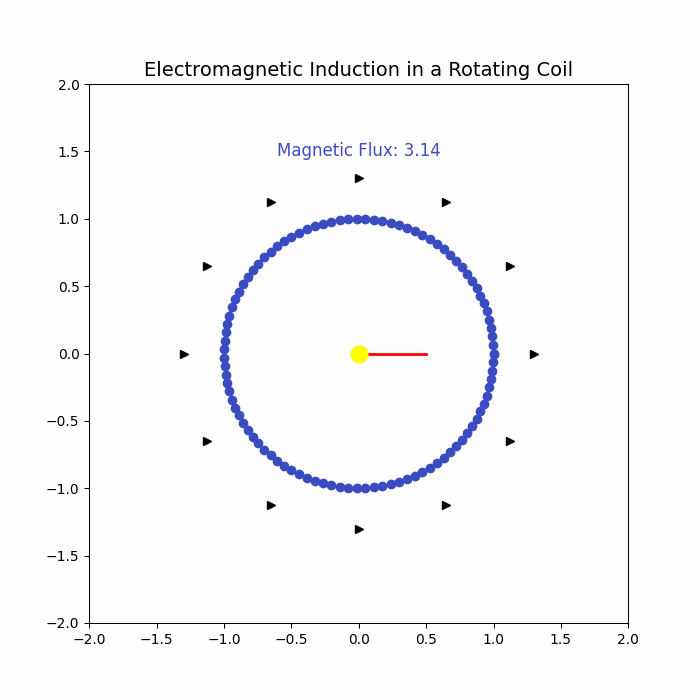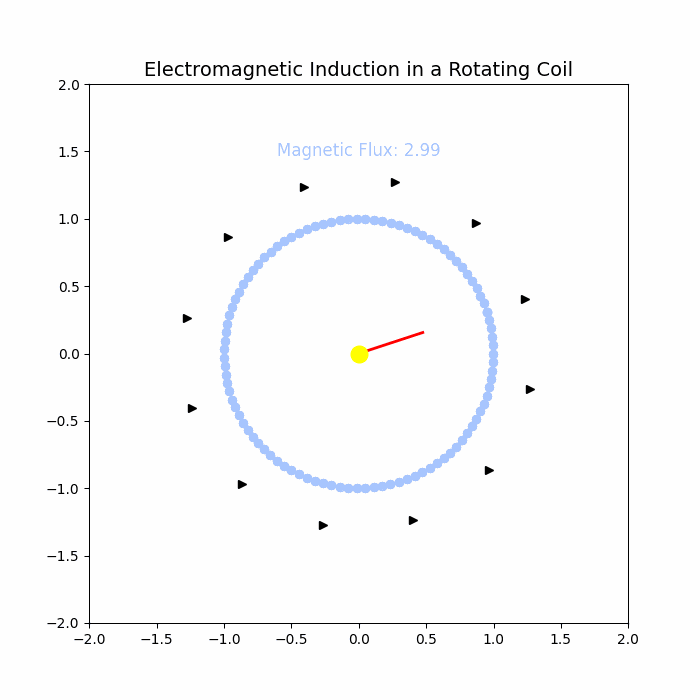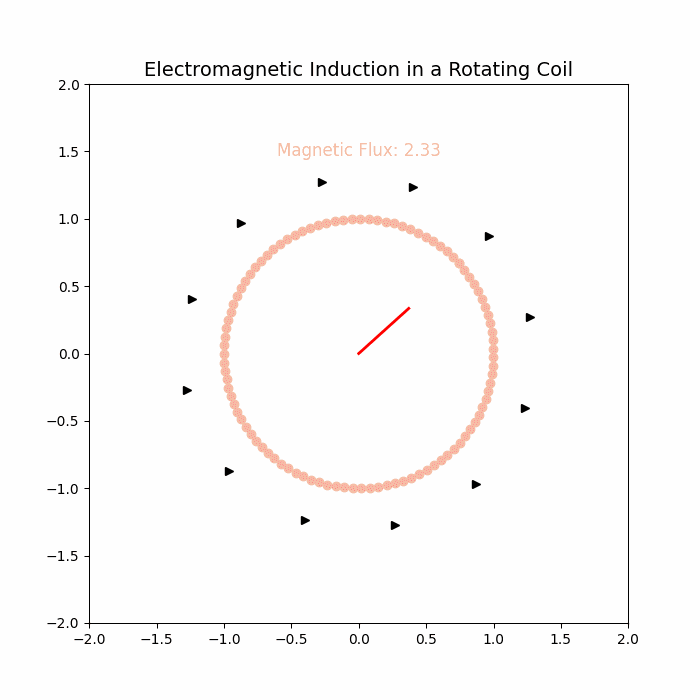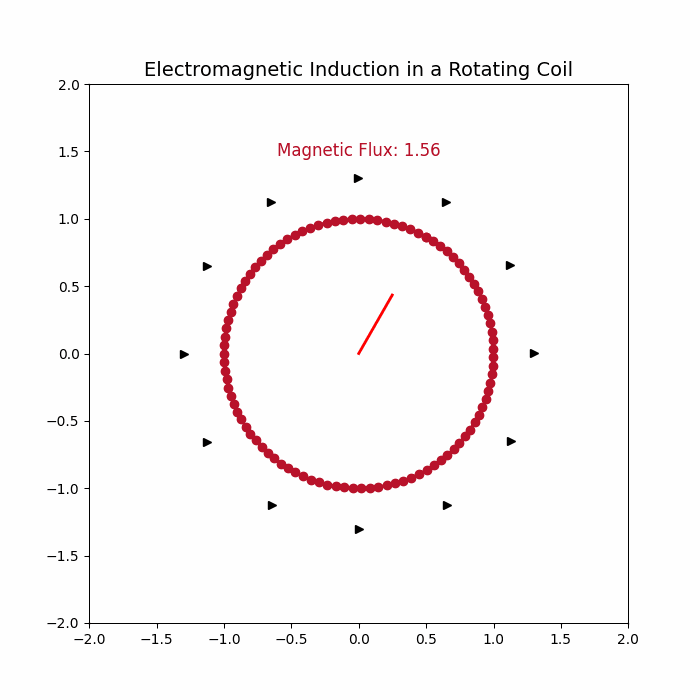
Electromagnetic Induction in a Rotating Coil

Nov 4, 2024 — Mejbah Ahammad

Electromagnetic induction is a fundamental principle of physics and electrical engineering, describing how a changing magnetic field can induce an electromotive force (EMF) in a conductor. Discovered by Michael Faraday in 1831, this phenomenon has paved the way for numerous technological advancements, including generators, transformers, and induction motors. A key application of electromagnetic induction is in a rotating coil within a magnetic field, which forms the basis of alternating current (AC) generators and many other devices.

Fundamental Concepts

💡 Faraday's Law of Electromagnetic Induction: Faraday's Law quantifies the induced EMF in a closed circuit due to a change in magnetic flux through the circuit. It states that the induced EMF is equal to the negative rate of change of magnetic flux:
$$ \mathcal{E} = -\dfrac{d\Phi_B}{dt} $$

Where:
- $ \mathcal{E} $ is the induced electromotive force (in volts).
- $ \Phi_B $ is the magnetic flux (in webers).
- The negative sign represents Lenz's Law, indicating the direction of the induced EMF opposes the change in flux.
📖 Magnetic Flux: Magnetic flux measures the quantity of magnetism, considering the strength and extent of a magnetic field. It is defined as:
$$ \Phi_B = \int \mathbf{B} \cdot d\mathbf{A} $$

For a uniform magnetic field passing perpendicularly through a flat surface:

$$ \Phi_B = B A \cos \theta $$

Where:
- $ B $ is the magnetic field strength (in teslas).
- $ A $ is the area through which the field lines pass (in square meters).
- $ \theta $ is the angle between the magnetic field and the normal to the surface.
🔬 Lenz's Law: Lenz's Law provides the direction of the induced current or EMF resulting from electromagnetic induction. It states that the induced EMF will generate a current whose magnetic field opposes the change in the original magnetic flux, ensuring the conservation of energy.

Electromagnetic Induction in a Rotating Coil

When a coil rotates within a magnetic field, the angle $ \theta $ between the magnetic field and the normal to the coil changes with time. This variation in $ \theta $ leads to a change in magnetic flux through the coil, inducing an EMF according to Faraday's Law. This is the fundamental operating principle of AC generators.

Mathematical Analysis

Consider a coil with $ N $ turns, each of area $ A $, rotating at a constant angular velocity $ \omega $ in a uniform magnetic field $ B $. The angle $ \theta $ at any time $ t $ is given by $ \theta = \omega t $.

Magnetic Flux Through the Coil

The magnetic flux $ \Phi_B $ through the coil at time $ t $ is:

$$ \Phi_B = N B A \cos (\omega t) $$

Induced EMF

Applying Faraday's Law, the induced EMF $ \mathcal{E} $ is:

\[ \begin{align*} \mathcal{E} &= -\dfrac{d\Phi_B}{dt} \\ &= -\dfrac{d}{dt} [N B A \cos (\omega t)] \\ &= N B A \omega \sin (\omega t) \end{align*} \]

This equation shows that the induced EMF varies sinusoidally with time, producing alternating current when connected in a closed circuit.

Factors Affecting Induced EMF

💡 Number of Turns ($ N $): The induced EMF is directly proportional to the number of turns in the coil. Increasing $ N $ amplifies the EMF because each loop contributes to the total voltage.
📖 Magnetic Field Strength ($ B $): A stronger magnetic field increases the rate of flux change, resulting in a higher induced EMF.
🔬 Area of the Coil ($ A $): Larger coil area allows more magnetic field lines to pass through, enhancing the magnetic flux and the induced EMF.
💡 Angular Velocity ($ \omega $): Higher angular velocity means the coil rotates faster, causing the magnetic flux to change more rapidly, thus increasing the induced EMF.

Applications of Electromagnetic Induction in Rotating Coils

Alternating Current (AC) Generators

AC generators, or alternators, convert mechanical energy into electrical energy using electromagnetic induction. The rotating coil in a magnetic field induces an EMF, producing an alternating voltage and current that varies sinusoidally over time.

Electric Motors

While motors primarily convert electrical energy into mechanical energy, they also rely on electromagnetic induction. In some types of motors, the rotation of the coil within a magnetic field induces currents that interact with the magnetic field to produce torque.

Transformers

Transformers use electromagnetic induction to transfer electrical energy between two or more coils (primary and secondary) without physical contact. Although transformers do not involve rotating coils, the principles of changing magnetic flux and induced EMF are the same.

Experimental Demonstration

Setup

An experiment to demonstrate electromagnetic induction in a rotating coil involves the following components:

A multi-turn coil of wire (preferably with enamel insulation).
A strong, uniform magnetic field, typically provided by permanent magnets or an electromagnet.
A mechanism to rotate the coil at varying speeds, such as a motor or hand crank.
A galvanometer or sensitive voltmeter to detect the induced EMF.

Procedure

Mount the coil so it can rotate freely within the magnetic field, ensuring the axis of rotation is perpendicular to the magnetic field lines.
Connect the ends of the coil to the galvanometer to measure the induced EMF.
Begin rotating the coil and observe the galvanometer's response.
Vary the rotation speed and note the changes in the induced EMF magnitude.

Observations

The galvanometer needle deflects in one direction and then the other as the coil rotates, indicating an alternating EMF. Faster rotation speeds result in greater deflections, demonstrating the direct relationship between angular velocity and induced EMF.

Real-World Examples

Hydroelectric Power Plants

In hydroelectric plants, flowing water drives turbines connected to large coils rotating within magnetic fields. The mechanical energy from the water's motion is converted into electrical energy via electromagnetic induction.

Wind Turbines

Wind turbines capture kinetic energy from wind to rotate coils or magnets, inducing EMF and generating electricity without fossil fuels.

Automotive Alternators

Alternators in vehicles charge the battery and power electrical systems. The engine's mechanical energy rotates the alternator's coil within a magnetic field, inducing an EMF that produces electrical current.

Mathematical Derivations

Maximum Induced EMF

The maximum EMF occurs when $ \sin (\omega t) = 1 $:

$$ \mathcal{E}_{\text{max}} = N B A \omega $$

RMS Value of Induced EMF

The root mean square (RMS) value is important for calculating average power in AC circuits:

$$ \mathcal{E}_{\text{rms}} = \dfrac{\mathcal{E}_{\text{max}}}{\sqrt{2}} = \dfrac{N B A \omega}{\sqrt{2}} $$

Induced Current and Power

If the coil forms a closed circuit with resistance $ R $, the induced current $ I $ is:

$$ I = \dfrac{\mathcal{E}}{R} = \dfrac{N B A \omega \sin (\omega t)}{R} $$

The instantaneous power delivered is:

$$ P = \mathcal{E} I = \dfrac{(N B A \omega \sin (\omega t))^2}{R} $$

Energy Considerations

The mechanical work done to rotate the coil is converted into electrical energy. According to the law of conservation of energy, the electrical power generated equals the mechanical power input minus any system losses (e.g., friction, heat).

Efficiency

The efficiency $ \eta $ of the energy conversion process is:

$$ \eta = \dfrac{P_{\text{out}}}{P_{\text{in}}} \times 100\% $$

Where:

$ P_{\text{out}} $ is the electrical power output.
$ P_{\text{in}} $ is the mechanical power input.

Advanced Topics

Eddy Currents

Eddy currents are loops of electric current induced within conductors by a changing magnetic field. They can cause energy losses due to resistive heating (Joule heating). To minimize eddy currents, laminated cores made of insulated layers of iron are used in transformers and motors.

Skin Effect

At high frequencies, alternating current tends to flow near the surface of conductors, a phenomenon known as the skin effect. This reduces the effective cross-sectional area available for current flow, increasing resistance and affecting the performance of coils in AC applications.

Back EMF in Motors

In electric motors, the rotation of the coil within a magnetic field induces a back EMF that opposes the applied voltage. This back EMF limits the current flow and is essential for the motor's speed regulation.

Self-Inductance

Self-inductance is the property of a coil whereby a change in current induces an EMF in the coil itself, opposing the change in current. This effect is significant in circuits with rapidly changing currents and must be considered in the design of inductive components.

Practical Considerations

Coil Design

Optimizing coil parameters enhances the efficiency of electromagnetic induction:

Core Material: Using ferromagnetic materials like iron increases magnetic field concentration.
Wire Gauge: Thicker wires reduce resistance but increase weight and size.
Number of Turns: More turns increase EMF but also resistance and inductance.
Cooling Mechanisms: To dissipate heat generated by resistive losses.

Frequency Considerations

The frequency of the induced EMF depends on the rotational speed of the coil. In power generation, standard frequencies (50 Hz or 60 Hz) are maintained to ensure compatibility with the electrical grid and appliances.

Losses and Efficiency

Several factors contribute to energy losses:

Resistive (Ohmic) Losses: Due to the inherent resistance of the coil wire.
Hysteresis Losses: Energy dissipated in the core material due to its magnetization and demagnetization cycle.
Eddy Current Losses: Induced currents in conductive parts of the core or structure, minimized by using laminated cores.
Mechanical Losses: Friction in bearings and air resistance (windage losses).

Safety Considerations

Handling devices that involve electromagnetic induction requires adherence to safety protocols:

Electrical Safety: High voltages can be induced; proper insulation and grounding are essential.
Mechanical Safety: Rotating parts should be enclosed to prevent injury from moving components.
Thermal Safety: Heat generated due to losses can cause burns or start fires; adequate cooling and temperature monitoring are necessary.
Magnetic Fields: Strong magnetic fields can affect pacemakers and other medical devices; warning signs should be posted.

Historical Context

The discovery of electromagnetic induction was a pivotal moment in the history of science. Michael Faraday's experiments in the early 19th century laid the groundwork for the electrical revolution.

Faraday's Experiments

Faraday conducted a series of experiments demonstrating that a changing magnetic field could induce an electric current. His work was contemporaneous with that of Joseph Henry, who made similar discoveries independently in the United States.

Impact on Technology

The principles of electromagnetic induction enabled the invention of electric generators and transformers, which are fundamental to modern power distribution systems. The ability to generate and transmit electricity efficiently has had profound implications for industry, transportation, and daily life.

Modern Developments

Superconducting Generators

Advancements in superconducting materials have led to the development of superconducting generators. These devices can generate large amounts of power with minimal resistive losses, improving efficiency.

Renewable Energy Integration

Electromagnetic induction plays a crucial role in harnessing renewable energy sources like wind and tidal power. Innovations in generator design are increasing the viability of these clean energy technologies.

Wireless Power Transfer

Electromagnetic induction is the basis for wireless charging technologies used in smartphones and electric vehicles. By inducing currents in coils without direct contact, power can be transferred over short distances safely and conveniently.

Future Perspectives

As technology advances, the applications of electromagnetic induction continue to expand:

Magnetic Levitation: Inductive principles are used in maglev trains, which float above tracks, reducing friction and allowing for high-speed transportation.
Smart Grids: Improved transformers and inductive components enhance the efficiency and reliability of electrical grids, integrating renewable energy sources seamlessly.
Medical Devices: Inductive charging and energy transfer are used in implanted medical devices, reducing the need for invasive procedures to replace batteries.

Educational Importance

Understanding electromagnetic induction is essential for students in physics and engineering fields. It provides a foundation for topics in electromagnetism, electronics, and power systems.

Laboratory Experiments

Experiments with rotating coils, transformers, and induction coils help students grasp the practical aspects of electromagnetic theory.

Problem-Solving Skills

Analyzing circuits involving inductance enhances analytical skills, preparing students for complex challenges in technology and research.

Conclusion

Electromagnetic induction in a rotating coil is a fundamental concept with wide-ranging applications in modern technology. From power generation to wireless communication, the principles discovered by Faraday continue to influence innovation and development.

The interplay between theoretical understanding and practical application exemplifies the importance of physics in advancing human capabilities. As we continue to explore and harness electromagnetic phenomena, the potential for new technologies and solutions to global challenges grows.

References

Serway, R. A., & Jewett, J. W. (2018). Physics for Scientists and Engineers (10th ed.). Cengage Learning.
Halliday, D., Resnick, R., & Walker, J. (2013). Fundamentals of Physics (10th ed.). Wiley.
Hambley, A. R. (2017). Electrical Engineering: Principles and Applications (7th ed.). Pearson.
Tipler, P. A., & Mosca, G. (2007). Physics for Scientists and Engineers (6th ed.). W.H. Freeman.
Fitzpatrick, R. (2008). Maxwell's Equations and the Principles of Electromagnetism. Infinity Science Press.

Glossary

Electromotive Force (EMF): A voltage generated by a battery or by the magnetic force according to Faraday's Law.
Magnetic Flux ($ \Phi_B $): The measure of the amount of magnetic field passing through a given area.
Angular Velocity ($ \omega $): The rate of change of angular position of a rotating body, measured in radians per second.
Inductor: A passive electrical component that stores energy in its magnetic field, often used in filters and oscillators.
Transformer: A device that transfers electrical energy between circuits through electromagnetic induction, typically used to increase or decrease voltage levels.
Eddy Currents: Circulating currents induced within conductors by changing magnetic fields, often causing energy losses.
Skin Effect: The tendency of alternating current to distribute within a conductor such that the current density is largest near the surface, decreasing at greater depths.
Self-Inductance: The property of a conductor by which a change in current induces an EMF in the conductor itself.
Hysteresis Loss: Energy loss in a magnetic material due to the lag between changes in magnetization and the magnetic field causing it.
Back EMF: The EMF induced in a motor's coil that opposes the applied voltage, limiting the current and regulating the motor's speed.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import matplotlib.cm as cm

# Parameters
B = 1.0  # Magnetic field strength
coil_radius = 1.0  # Radius of the coil
num_points = 100  # Points to define the coil
rotation_speed = 0.1  # Speed of rotation of the coil (in radians per frame)
num_frames = 200  # Total frames for the animation

# Calculate coil area
A = np.pi * coil_radius**2

# Define a circle for the coil
theta = np.linspace(0, 2 * np.pi, num_points)
x_coil = coil_radius * np.cos(theta)
y_coil = coil_radius * np.sin(theta)

# Set up the figure
fig, ax = plt.subplots(figsize=(7, 7))
ax.set_xlim(-2, 2)
ax.set_ylim(-2, 2)
ax.set_aspect('equal')
ax.set_title("Electromagnetic Induction in a Rotating Coil", fontsize=14)

# Initialize plot elements
coil_line, = ax.plot([], [], 'o-', lw=2, color='blue')
flux_text = ax.text(0, 1.5, '', ha='center', va='center', fontsize=12, color='purple')
flux_arrow, = ax.plot([], [], color='red', lw=2)  # Magnetic field arrow
current_arrows = [ax.plot([], [], 'o', color='black')[0] for _ in range(12)]  # Induced current arrows
spark, = ax.plot([], [], 'o', color='yellow', markersize=12, alpha=0)  # Spark effect

# Color gradient for flux lines
cmap = cm.coolwarm
flux_colors = cmap(np.linspace(0, 1, num_frames))

# Initialization function
def init():
    coil_line.set_data([], [])
    flux_arrow.set_data([], [])
    flux_text.set_text('')
    spark.set_alpha(0)
    for arrow in current_arrows:
        arrow.set_data([], [])
    return [coil_line, flux_text, flux_arrow, spark] + current_arrows

# Update function for animation
def update(frame):
    # Rotate the coil by changing the angle
    angle = rotation_speed * frame
    x_rotated = x_coil * np.cos(angle) - y_coil * np.sin(angle)
    y_rotated = x_coil * np.sin(angle) + y_coil * np.cos(angle)
    coil_line.set_data(x_rotated, y_rotated)
    coil_line.set_color(flux_colors[frame])  # Change color based on flux intensity

    # Calculate magnetic flux through the coil
    flux = B * A * np.cos(angle)
    flux_text.set_text(f"Magnetic Flux: {flux:.2f}")
    flux_text.set_color(flux_colors[frame])  # Change text color with flux

    # Draw an arrow representing the magnetic field direction
    flux_arrow.set_data([0, 0.5 * np.cos(angle)], [0, 0.5 * np.sin(angle)])

    # Update current arrows around the coil to show induced current
    for i, arrow in enumerate(current_arrows):
        # Arrange arrows in a circle around the coil
        arrow_angle = i * (2 * np.pi / len(current_arrows)) + angle
        x_arrow = (coil_radius + 0.3) * np.cos(arrow_angle)
        y_arrow = (coil_radius + 0.3) * np.sin(arrow_angle)
        arrow.set_data(x_arrow, y_arrow)
        # Flip the direction based on flux change
        arrow.set_marker('>' if np.cos(angle) > 0 else '<')

    # Electric spark effect at flux peaks
    if abs(flux) > 0.9 * B * A:
        spark.set_data(0, 0)  # Position at the center
        spark.set_alpha(1)  # Show spark
    else:
        spark.set_alpha(0)  # Hide spark

    return [coil_line, flux_text, flux_arrow, spark] + current_arrows

# Create the animation
ani = FuncAnimation(fig, update, frames=num_frames, init_func=init, interval=30, blit=True)

# Display the animation
plt.show()

# Save the animation as GIF
ani.save('electromagnetic_induction_coil.gif', writer='pillow', fps=30)