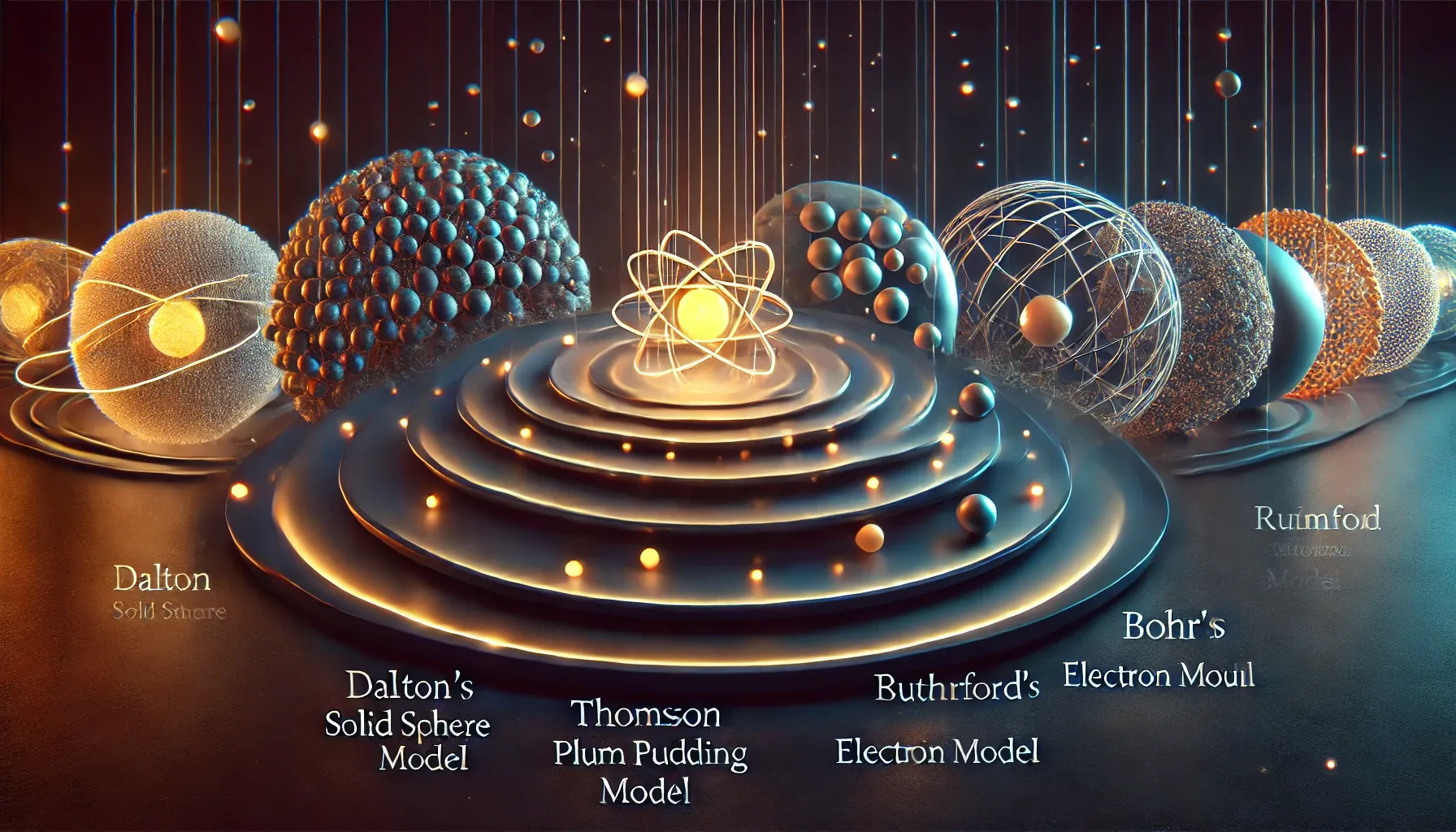
The atomic model is a theoretical framework that describes the structure and behavior of atoms, the fundamental building blocks of matter. Over centuries, scientists have developed various models to explain the nature of atoms, each building upon the discoveries and limitations of its predecessors. Understanding atomic models is essential in fields such as chemistry, physics, and material science, providing insights into the composition of matter and the interactions between particles.
Fundamental Concepts
-
💡 Dalton's Atomic Theory: Proposed by John Dalton in the early 19th century, Dalton's atomic theory laid the foundation for modern chemistry by asserting that matter is composed of indivisible atoms. Dalton's key postulates include:
- All matter is made of indivisible atoms.
- All atoms of a given element are identical in mass and properties.
- Compounds are formed by a combination of two or more different types of atoms.
- A chemical reaction involves the rearrangement of atoms.
-
📖 Thomson's Plum Pudding Model: J.J. Thomson discovered the electron in 1897, leading him to propose a new atomic model. In this model:
- The atom is a positively charged sphere.
- Electrons are embedded within this positive charge, much like plums in a pudding.
- This model suggested that atoms are divisible into smaller particles.
-
🔬 Rutherford's Nuclear Model: Ernest Rutherford, through his gold foil experiment in 1909, provided evidence for a new atomic structure:
- Atoms have a small, dense, positively charged nucleus at the center.
- Electrons orbit the nucleus at relatively large distances.
- The majority of an atom's mass is concentrated in the nucleus.
- This model explained the scattering of alpha particles in the gold foil experiment.
Development of Atomic Models
The evolution of atomic models reflects the progressive understanding of atomic structure through experimental discoveries and theoretical advancements. Each model addressed the shortcomings of its predecessors, incorporating new findings to provide a more accurate representation of the atom.
Dalton's Atomic Theory
John Dalton's atomic theory was groundbreaking as it provided the first scientific explanation for the nature of matter. Dalton proposed that each element is composed of unique atoms and that chemical reactions involve the rearrangement of these atoms. However, his model did not account for the internal structure of atoms or the existence of subatomic particles.
Thomson's Plum Pudding Model
The discovery of the electron by J.J. Thomson led to the plum pudding model, which introduced the idea that atoms are not indivisible but contain smaller charged particles. This model was significant as it challenged Dalton's notion of indivisible atoms and paved the way for further exploration into atomic structure.
Rutherford's Nuclear Model
Ernest Rutherford's gold foil experiment revealed that atoms have a small, dense nucleus surrounded by electrons. This model shifted the focus from the diffuse positive charge of the plum pudding model to a centralized nucleus, laying the groundwork for the modern understanding of the atom's internal structure.
Bohr's Planetary Model
Niels Bohr refined Rutherford's model by introducing quantized electron orbits. According to Bohr, electrons orbit the nucleus in specific energy levels, and transitions between these levels result in the emission or absorption of energy. This model successfully explained the spectral lines of hydrogen but was limited in explaining more complex atoms.
Quantum Mechanical Model
The quantum mechanical model, developed by scientists such as Schrödinger and Heisenberg, describes electrons in terms of probability distributions rather than fixed orbits. This model incorporates the principles of quantum mechanics, providing a more accurate and comprehensive understanding of atomic behavior, especially for multi-electron systems.
Detailed Analysis of Atomic Models
Dalton's Atomic Theory
Dalton's atomic theory comprised several key principles:
- All matter is composed of atoms, which are indivisible and indestructible.
- All atoms of a particular element are identical in mass and properties.
- Atoms of different elements can combine in simple whole-number ratios to form compounds.
- A chemical reaction involves the rearrangement of atoms; atoms are neither created nor destroyed.
While Dalton's theory provided a solid foundation, it failed to explain the existence of isotopes, subatomic particles, and the behavior of electrons in atoms.
Thomson's Plum Pudding Model
J.J. Thomson's discovery of the electron led him to propose the plum pudding model. In this model:
- The atom is a positively charged sphere.
- Electrons are scattered within the positive charge, balancing the overall charge.
- The model suggested that atoms are divisible, containing smaller charged particles.
While this model introduced the concept of internal structure, it could not explain the results of Rutherford's gold foil experiment, which indicated the presence of a concentrated nucleus.
Rutherford's Nuclear Model
Ernest Rutherford's gold foil experiment provided critical insights into atomic structure:
- Most alpha particles passed through the gold foil with little or no deflection, indicating that atoms are mostly empty space.
- A few alpha particles were deflected at large angles, suggesting a small, dense, positively charged nucleus.
- Electrons orbit the nucleus, occupying the vast majority of the atom's volume.
This model marked a significant shift from the plum pudding model, emphasizing the importance of the nucleus in atomic structure.
Bohr's Planetary Model
Niels Bohr introduced quantized electron orbits to address the limitations of Rutherford's model:
- Electrons occupy specific energy levels or shells around the nucleus.
- Electrons can transition between energy levels by absorbing or emitting discrete amounts of energy (quanta).
- The model successfully explained the spectral lines of hydrogen but struggled with more complex atoms.
Bohr's model bridged the gap between classical and quantum physics, laying the groundwork for the development of the quantum mechanical model.
Quantum Mechanical Model
The quantum mechanical model provides the most accurate description of atomic structure:
- Electrons are described by wavefunctions, representing probability distributions rather than fixed orbits.
- Electron positions and momenta cannot be simultaneously determined with arbitrary precision (Heisenberg Uncertainty Principle).
- Orbitals are regions of space where electrons are likely to be found, characterized by specific energy levels and shapes.
- The model accounts for electron spin and the Pauli Exclusion Principle, explaining the arrangement of electrons in multi-electron atoms.
This model effectively explains the chemical behavior of elements, the structure of the periodic table, and the properties of materials at the atomic level.
Comparative Analysis of Atomic Models
Each atomic model offers a unique perspective on the structure and behavior of atoms, addressing the limitations of previous models while introducing new concepts:
| Model | Key Features | Strengths | Limitations |
|---|---|---|---|
| Dalton's Atomic Theory | Indivisible atoms, identical atoms for each element, atoms combine in whole numbers | Foundation for modern chemistry, explained laws of chemical combination | Did not account for subatomic particles, isotopes, or electron behavior |
| Thomson's Plum Pudding Model | Positive sphere with embedded electrons | Introduced internal structure of atoms, explained electrical neutrality | Could not explain gold foil experiment results, lacked a central nucleus |
| Rutherford's Nuclear Model | Small, dense nucleus with electrons orbiting | Explained scattering of alpha particles, introduced nucleus | Could not explain electron stability or spectral lines |
| Bohr's Planetary Model | Quantized electron orbits, energy levels | Explained hydrogen spectral lines, introduced quantization | Limited to single-electron systems, did not account for electron-electron interactions |
| Quantum Mechanical Model | Electron probability distributions, orbitals, quantum numbers | Accurate description of multi-electron atoms, explains chemical behavior and material properties | Mathematically complex, less intuitive than earlier models |
Experimental Evidence Supporting Atomic Models
Various experiments have provided evidence supporting the different atomic models:
- 💡 Dalton's Law of Multiple Proportions: Demonstrated that elements combine in fixed ratios, supporting the idea of indivisible atoms.
- 📖 Thomson's Cathode Ray Tube Experiment: Showed the presence of electrons, leading to the plum pudding model.
- 🔬 Rutherford's Gold Foil Experiment: Provided evidence for a central nucleus, leading to the nuclear model.
- 💡 Bohr's Hydrogen Spectrum Analysis: Explained the discrete spectral lines of hydrogen, supporting the quantized orbit model.
- 📖 Electron Diffraction Experiments: Supported the wave-particle duality of electrons, reinforcing the quantum mechanical model.
Modern Atomic Theory
The modern atomic theory incorporates the principles of quantum mechanics to provide a comprehensive understanding of atomic structure:
- 💡 Quantum Numbers: Describe the properties of atomic orbitals and the properties of electrons in orbitals.
- 📖 Electron Spin: An intrinsic form of angular momentum carried by electrons, leading to the concept of spin quantum number.
- 🔬 Pauli Exclusion Principle: No two electrons in an atom can have the same set of four quantum numbers, explaining electron configuration in atoms.
The modern atomic theory provides a robust framework for understanding chemical bonding, spectroscopy, and the periodic properties of elements.
Applications of Atomic Models
Chemical Bonding
Atomic models are essential in explaining how atoms interact and bond to form molecules. The quantum mechanical model, in particular, provides insights into covalent, ionic, and metallic bonds by describing the behavior of electrons in different orbital configurations.
Spectroscopy
Understanding atomic models allows scientists to interpret spectral lines, which are crucial in identifying elements and studying atomic transitions. Spectroscopy has applications in fields ranging from astronomy to forensic science.
Material Science
Atomic models help in designing materials with specific properties by understanding the arrangement and behavior of atoms within solids, liquids, and gases. This knowledge is vital in developing new alloys, semiconductors, and nanomaterials.
Historical Context
The development of atomic models has been driven by experimental discoveries and theoretical advancements. Each model has played a crucial role in advancing our understanding of matter:
- 💡 Dalton's Era: Laid the foundation for atomic theory, influencing early chemistry and the study of chemical reactions.
- 📖 Thomson and Rutherford: Introduced subatomic particles and the concept of the atomic nucleus, revolutionizing the understanding of atomic structure.
- 🔬 Bohr and Quantum Mechanics: Provided a more detailed and accurate description of atomic structure, leading to the modern atomic model.
Modern Developments
Quantum Computing
Advancements in understanding atomic and subatomic particles have paved the way for quantum computing, which leverages the principles of quantum mechanics to perform complex computations more efficiently than classical computers.
Nanotechnology
Atomic models are fundamental in nanotechnology, where manipulation of individual atoms and molecules is essential for creating nanoscale materials and devices with unique properties.
Medical Imaging
Techniques like MRI and PET scans rely on principles derived from atomic and quantum models to provide detailed images of the body's internal structures, aiding in diagnosis and treatment.
Future Perspectives
As scientific knowledge advances, atomic models continue to evolve, offering deeper insights into the nature of matter and unlocking new technological possibilities:
- Advanced Particle Physics: Continued research into atomic and subatomic particles will further refine atomic models, potentially leading to new discoveries in fundamental physics.
- Energy Solutions: Understanding atomic interactions is crucial for developing sustainable energy sources, such as fusion reactors and advanced photovoltaic cells.
- Environmental Science: Atomic models aid in understanding pollutant behavior and developing technologies for environmental protection and remediation.
Educational Importance
Atomic models are a cornerstone of education in the sciences, providing students with a framework to understand complex concepts in chemistry, physics, and biology. Mastery of atomic models fosters critical thinking and problem-solving skills essential for scientific inquiry and innovation.
Laboratory Experiments
Hands-on experiments with atomic models, such as spectroscopy and electron microscopy, help students visualize and comprehend the abstract concepts of atomic structure and behavior.
Interdisciplinary Learning
Atomic models bridge various scientific disciplines, illustrating the interconnectedness of physics, chemistry, and biology. This interdisciplinary approach enhances students' ability to integrate knowledge across different fields.
Conclusion
The atomic model is a fundamental concept that has evolved through centuries of scientific discovery and theoretical refinement. From Dalton's indivisible atoms to the sophisticated quantum mechanical model, each advancement has deepened our understanding of the fundamental building blocks of matter. This progression not only enhances our knowledge of the natural world but also drives technological innovation across multiple disciplines.
As research continues, atomic models will undoubtedly undergo further refinement, offering even more precise insights into the nature of atoms and their interactions. This ongoing development underscores the dynamic and ever-evolving nature of scientific inquiry, highlighting the importance of atomic models in both theoretical and applied sciences.
References
- Serway, R. A., & Jewett, J. W. (2018). Physics for Scientists and Engineers (10th ed.). Cengage Learning.
- Halliday, D., Resnick, R., & Walker, J. (2013). Fundamentals of Physics (10th ed.). Wiley.
- Hambley, A. R. (2017). Electrical Engineering: Principles and Applications (7th ed.). Pearson.
- Tipler, P. A., & Mosca, G. (2007). Physics for Scientists and Engineers (6th ed.). W.H. Freeman.
- Fitzpatrick, R. (2008). Maxwell's Equations and the Principles of Electromagnetism. Infinity Science Press.
- McMurry, J., Fay, R., & Robinson, L. (2016). Chemistry: The Central Science (14th ed.). Pearson.
- Griffiths, D. J. (2018). Introduction to Electrodynamics (4th ed.). Cambridge University Press.
- Hecht, E. (2017). Optics (5th ed.). Pearson.
- Peterson, B. N. (2016). Modern Physics (6th ed.). Wiley.
- Brown, T. L., LeMay, H. E., Bursten, B. E., & Murphy, C. J. (2018). Chemistry: The Central Science (14th ed.). Pearson.
Glossary
- Atomic Number (Z): The number of protons in the nucleus of an atom, defining the element.
- Mass Number (A): The total number of protons and neutrons in an atom's nucleus.
- Isotope: Variants of an element with the same number of protons but different numbers of neutrons.
- Electron Cloud: The region around the nucleus where electrons are likely to be found, described by probability distributions.
- Orbital: A region of space within an atom where an electron is likely to be found, characterized by quantum numbers.
- Quantum Numbers: Numbers that describe the properties of atomic orbitals and the electrons in them, including energy level, shape, orientation, and spin.
- Pauli Exclusion Principle: States that no two electrons in an atom can have the same set of four quantum numbers.
- Electron Spin: An intrinsic form of angular momentum carried by electrons, contributing to their magnetic moment.
- Hybridization: The process of mixing atomic orbitals to form new hybrid orbitals suitable for pairing electrons in chemical bonds.
- Covalent Bond: A chemical bond formed by the sharing of electrons between atoms.
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation, PillowWriter
# Initialize the figure and axis
fig, ax = plt.subplots(figsize=(8, 6))
# Draw nucleus function to create protons and neutrons
def draw_nucleus(center_x, center_y):
proton_positions = [(-0.15, -0.15), (0.15, 0.15), (-0.15, 0.15), (0.15, -0.15)]
neutron_positions = [(0, 0.15), (0, -0.15), (0.15, 0), (-0.15, 0)]
protons, neutrons = [], []
for dx, dy in proton_positions:
proton, = ax.plot([], [], 'b+', markersize=12)
protons.append((proton, [center_x + dx], [center_y + dy]))
for dx, dy in neutron_positions:
neutron, = ax.plot([], [], 'ro', markersize=10)
neutrons.append((neutron, [center_x + dx], [center_y + dy]))
return protons + neutrons
# Function to draw an electron shell
def draw_shell(center_x, center_y, radius, num_electrons, n_level, label_offset=(0, 0)):
shell_circle = plt.Circle((center_x, center_y), radius, color="gray", linestyle="--", fill=False, lw=1.2)
ax.add_artist(shell_circle)
angles = np.linspace(0, 2 * np.pi, num_electrons, endpoint=False)
electrons = []
for angle in angles:
x = center_x + radius * np.cos(angle)
y = center_y + radius * np.sin(angle)
electron, = ax.plot([], [], 'go', markersize=8)
electrons.append((electron, [x], [y]))
# Label the energy level (n)
label = ax.text(center_x + radius * 1.15 + label_offset[0], center_y + label_offset[1], f"n = {n_level}",
ha='center', va='center', fontsize=10, color="black", visible=False)
return electrons, label
# Prepare atomic models with shells for animation
left_protons_neutrons = draw_nucleus(-4, 0)
left_shell_1, left_label_1 = draw_shell(-4, 0, 1.5, 2, 1, label_offset=(0.3, 0))
left_shell_2, left_label_2 = draw_shell(-4, 0, 3, 8, 2, label_offset=(0.6, 0))
left_shell_3, left_label_3 = draw_shell(-4, 0, 4.5, 18, 3, label_offset=(0.9, 0))
right_protons_neutrons = draw_nucleus(4, 0)
right_shell_1, right_label_1 = draw_shell(4, 0, 1.5, 2, 1, label_offset=(0.3, 0))
right_shell_2, right_label_2 = draw_shell(4, 0, 3, 8, 2, label_offset=(0.6, 0))
right_shell_3, right_label_3 = draw_shell(4, 0, 4.5, 18, 3, label_offset=(0.9, 0))
# Combine all elements
all_elements = (left_protons_neutrons + left_shell_1 + left_shell_2 + left_shell_3 +
right_protons_neutrons + right_shell_1 + right_shell_2 + right_shell_3)
all_labels = [left_label_1, left_label_2, left_label_3, right_label_1, right_label_2, right_label_3]
# Dynamic annotation for each frame
annotation = ax.text(0, -5, "", ha='center', fontsize=12, color="black", bbox=dict(facecolor="lightyellow", edgecolor="black"))
# Legend for particles
plt.scatter([], [], color='blue', label='Protons', marker='+', s=100)
plt.scatter([], [], color='red', label='Neutrons', marker='o', s=100)
plt.scatter([], [], color='green', label='Electrons', s=100)
plt.legend(loc='lower left', fontsize=10)
# Set plot limits and hide axes for a clean look
ax.set_xlim(-8, 8)
ax.set_ylim(-6, 6)
ax.axis('off')
# Animation function to update elements per frame
def update(frame):
total_elements = len(all_elements)
if frame < total_elements:
# First half: Build the left atom
element, x, y = all_elements[frame]
element.set_data(x, y)
if frame < len(left_protons_neutrons):
annotation.set_text("Adding protons and neutrons to the nucleus")
elif frame < len(left_protons_neutrons) + len(left_shell_1):
annotation.set_text("Populating the first electron shell (n=1)")
all_labels[0].set_visible(True)
elif frame < len(left_protons_neutrons) + len(left_shell_1) + len(left_shell_2):
annotation.set_text("Populating the second electron shell (n=2)")
all_labels[1].set_visible(True)
elif frame < len(left_protons_neutrons) + len(left_shell_1) + len(left_shell_2) + len(left_shell_3):
annotation.set_text("Populating the third electron shell (n=3)")
all_labels[2].set_visible(True)
elif frame < total_elements * 2:
# Second half: Build the right atom
right_frame = frame - total_elements
element, x, y = all_elements[right_frame]
element.set_data(x, y)
if right_frame < len(right_protons_neutrons):
annotation.set_text("Adding protons and neutrons to the second nucleus")
elif right_frame < len(right_protons_neutrons) + len(right_shell_1):
annotation.set_text("Populating the first electron shell on the right (n=1)")
all_labels[3].set_visible(True)
elif right_frame < len(right_protons_neutrons) + len(right_shell_1) + len(right_shell_2):
annotation.set_text("Populating the second electron shell on the right (n=2)")
all_labels[4].set_visible(True)
elif right_frame < len(right_protons_neutrons) + len(right_shell_1) + len(right_shell_2) + len(right_shell_3):
annotation.set_text("Populating the third electron shell on the right (n=3)")
all_labels[5].set_visible(True)
# Create the animation
ani = FuncAnimation(fig, update, frames=len(all_elements) * 2, interval=100, repeat=False)
# Save the animation as a GIF
ani.save('dynamic_atomic_model.gif', writer=PillowWriter(fps=10))
# Display the plot (optional)
plt.show()