Projectile Motion | Physics

What is Projectile Motion?

Projectile motion refers to the motion of an object thrown or projected into the air under the action of gravity. Once in motion, the object, called a projectile, moves along a curved path under the influence of two forces:

1. The initial velocity imparted to the object (horizontal and vertical components).
2. The force of gravity, which acts downward.

Projectile motion is a classic example of two-dimensional motion because it involves movement in both horizontal and vertical directions.

Components of Projectile Motion

1. Horizontal Component:
   • The horizontal motion occurs at a constant velocity because there are no horizontal forces acting on the projectile (assuming air resistance is neglected).
   • The horizontal displacement at any time ( t ) is given by:
     $$x(t) = v_{0x} \cdot t$$
     where \(v_{0x} = v_0 \cos(\theta)\) is the horizontal component of the initial velocity \( v_0\).
2. Vertical Component:
   • The vertical motion is affected by gravity, which causes the projectile to accelerate downward. This makes the vertical velocity change over time.
   • The vertical displacement at any time ( t ) is given by:
     $$y(t) = v_{0y} \cdot t - \frac{1}{2} g t^2$$
     where\( v_{0y} = v_0 \sin(\theta)\) is the vertical component of the initial velocity, and ( g ) is the acceleration due to gravity (approximately \(9.8 , \text{m/s}^2 )\).
3. Resultant Path:
   • The combination of constant horizontal motion and vertically accelerated motion results in a parabolic trajectory.
   • The general equation for the trajectory is:
     $$y(x) = \tan(\theta) \cdot x - \frac{g}{2 v_{0x}^2} \cdot x^2$$

Key Parameters in Projectile Motion

1. Time of Flight:
   • The total time the projectile remains in the air is called the time of flight. For a projectile launched and landing at the same height:
     $$T = \frac{2 v_0 \sin(\theta)}{g}$$
2. Maximum Height:
   • The highest vertical position reached by the projectile is called the maximum height:
     $$H = \frac{v_0^2 \sin^2(\theta)}{2g}$$
3. Range:
   • The horizontal distance the projectile travels is called the range. For a projectile launched and landing at the same height:
     $$R = \frac{v_0^2 \sin(2\theta)}{g}$$

Conditions for Symmetrical Projectile Motion

• Symmetrical motion occurs when the projectile is launched and lands at the same height. The path is symmetrical, meaning the ascent time equals the descent time.
• For symmetrical motion:
  • The time to reach the maximum height is half of the total time of flight:
    $$T_{max} = \frac{v_0 \sin(\theta)}{g}$$
  • The vertical velocity at the highest point is zero:
    $$v_y = 0$$

Real-Life Examples of Projectile Motion

• A ball being thrown, kicked, or hit in sports.
• A cannonball being fired from a cannon.
• Water fountains, where the water follows a parabolic trajectory.

In summary, projectile motion is a type of motion that results from an initial force, where the object follows a curved path under the influence of gravity. The motion can be broken down into horizontal and vertical components, which can be analyzed independently to predict the object's path, height, time of flight, and range. By breaking down the motion into horizontal and vertical components, we can solve for various aspects of the projectile's trajectory.

import math
import matplotlib.pyplot as plt

# Function to calculate the trajectory
def calculate_trajectory(v0, angle, g=9.81):
    # Convert angle to radians
    angle_rad = math.radians(angle)
    
    # Time of flight
    t_flight = 2 * v0 * math.sin(angle_rad) / g
    
    # Time intervals
    t_intervals = [i * 0.01 for i in range(int(t_flight / 0.01) + 1)]
    
    # X and Y coordinates of the projectile
    x = [v0 * math.cos(angle_rad) * t for t in t_intervals]
    y = [(v0 * math.sin(angle_rad) * t - 0.5 * g * t**2) for t in t_intervals]
    
    return x, y

# Initial velocity (m/s) and angle (degrees)
v0 = 20
angle = 45

# Calculate trajectory
x, y = calculate_trajectory(v0, angle)

# Plotting the trajectory
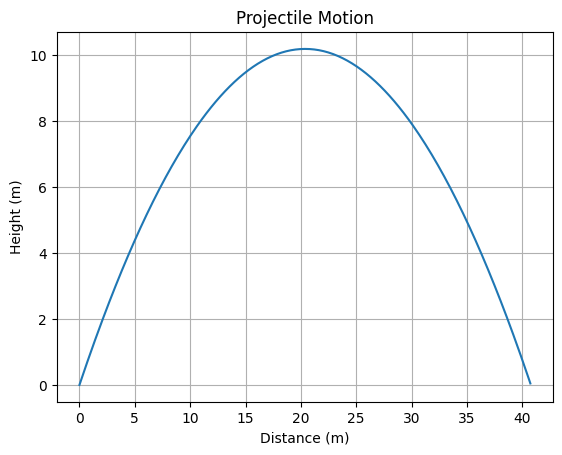
plt.plot(x, y)
plt.title("Projectile Motion")
plt.xlabel("Distance (m)")
plt.ylabel("Height (m)")
plt.grid(True)
plt.show()

Line 9: We calculate the time of flight t_flight using the formula .